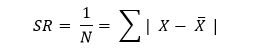Kemiringan Dan Keruncingan Data

Kemiringan Distribusi Data (Skewness)

Merupakan derajat atau ukuran dari ketidaksimetrisan

(Asimetri) suatu distribusi data.

Kemiringan distribusi data terdapat 3 jenis, yaitu :

Simetris : menunjukkan letak nilai rata-rata hitung,
median, dan modus berhimpit (berkisar

disatu titik)

Miring ke kanan : mempunyai nilai modus paling

kecil dan rata-rata hitung paling

besar

Miring ke kiri : mempunyai nilai modus paling besar

dan rata-rata hitung paling kecil

Ukuran Variansi Dan Simpang Baku

Pengertian Varians

    Varians adalah salah satu ukuran dispersi atau ukuran variasi.  Varians dapat menggambarkan bagaimana berpencarnya suatu data kuantitatif.  Varians diberi simbol  σ2 (baca: sigma kuadrat) untuk populasi dan untuk s2 sampel. 

Selanjutnya kita akan menggunakan simbol s2  untuk varians karena umumnya kita hampir selalu berkutat dengan sampel dan jarang sekali berkecimpung dengan populasi.

Rumus untuk menghitung varians ada dua , yaitu rumus teoritis dan rumus  kerja.  Namun demikian, untuk mempersingkat  tulisan ini, maka kita gunakan rumus kerja saja.  Rumus kerja ini mempunyai kelebihan dibandingkan rumus teoritis, yaitu hasilnya lebih akurat dan lebih mudah mengerjakannya.

Pengertian Simpangan Baku

   ukuran sebaran statistik yang paling lazim. Singkatnya, ia mengukur bagaimana nilai-nilai data tersebar. Bisa juga didefinisikan sebagai, rata-rata jarak penyimpangan titik-titik data diukur dari nilai rata-rata data tersebut. Di Indonesia sendiri simpangan baku juga biasa disebut dengan deviasi standar.

   Simpangan baku didefinisikan sebagai akar kuadrat varians. Simpangan baku merupakan bilangan tak-negatif, dan memiliki satuan yang sama dengan data. Misalnya jika suatu data diukur dalam satuan meter, maka simpangan baku juga diukur dalam meter pula. Istilah rumus simpangan bakupertama kali diperkenakan oleh Karl Pearson pada tahun 1894, dalam bukunya On the dissection of asymmetrical frequency curves.

   Dalam Statistik, wilayah data yang berada di antara +/- 1 simpangan baku akan berkisar 68.2%, wilayah data yang berada di antara +/- 2 simpangan baku akan berkisar 95.4%, dan wilayah data yang berada di antara +/- 3 simpangan baku akan berkisar 99.7%.

1. Jangkauan (Range)

Dik kelompok data :

• Kelompok data 1:

30,30,30,30,30     Maka R = 30-30 = 0

• Kelompok data 2 :

65,66,67,68,70    Maka R = 70-65 =5

• Kelompok data 3 :

50,60,70,80,90,100 Maka R = 100-50 = 50



2. Simpangan Rata-Rata

• 

Dik data = 5,10,15,20,25
       N     = 5

• 

Simpangan rata-rata =

3. Variansi dan Simpangan Baku (Variance dan Standard Deviation)

Variansi merupakan rata-rata kuadrat selisih atau kuadrat simpangan dari semua nilai data terhadap rata-rata hitung dan Simpangan Baku Merupakan akar pangkat dua dari variasi.

 4. Jangkauan Kuartil

Disebut juga simpangan kuartil atau rentang semi antar kuartil atau deviasi kuartil.

 

 

 

5. Jangkauan Persentil

 

UKURAN GEJALA PUSAT DATA DIKELOMPOKKAN

UKURAN GEJALA PUSAT DATA DIKELOMPOKKAN

     Ukuran gejala pusat merupakan suatu bilangan yang menunjukan sekitar dimana bilangan – bilangan yang ada dalam kumpulan data, oleh karenanya ukuran gejala pusat ini sering disebut dengan harga rata – rata. Harga rata – rata dari sekelompok data itu diharapkan dapat diwakili seluruh harga – harga yang ada dalam sekelompok data itu.
    Sebelum membahas hal ini, perlu diperjelas tentang apa yang dimaksud dengan data yang dikelompokkan dan data yang tidak dikelompokkan. Data yang dikelompokkan adalah data yang sudah disusun ke dalam sebuah distribusi frekuensi sehingga data tersebut mempunyai interval kelas yang jelas, mempunyai titik tengah kelas sedangkan data yang tidak dikelompokkan adalah data yang tidak disusun ke dalam distribusi frekuensi sehingga tidak mempunyai interval kelas dan titik tengah kelas.
    Mean, Median, Modus sama-sama merupakan ukuran pemusatan data yang termasuk kedalam analisis statistika deskriptif. Namun, ketiganya memiliki kelebihan dan kekurangannya masing-masing dalam menerangkan suatu ukuran pemusatan data. Untuk tahu kegunaannya masing-masing dan kapan kita mempergunakannya, perlu diketahui terlebih dahulu pengertian analisis statistika deskriptif dan ukuran pemusatan data.Contohnya yaitu :

Kelas	Nilai Statistik	Frekuensi	Titik tengah (m)	f.m	Frekuensi Kumulatif <
1	10 - 22	13	16	208	13
2	23 - 35	11	29	319	24
3	36 - 48	5	42	210	29
4	49 - 61	9	55	495	38
5	62 - 74	5	68	340	43
6	75 - 87	1	81	81	81
7	88 - 100	6	94	564	50
	Jumlah	50		2217
			44,34

• Mean (Rata – Rata Hitung)

Dalam istilah sehari – hari, mean dikenal dengan sebutan angka rata – rata, ada dua macam mean yang di bicarakan yaitu : mean untuk data yang tidak dikelompokkan dan mean untuk data yang dikelompokan. Mean adalah total semua data dibagi jumlah data. Mean digunakan ketika data yang kita miliki memiliki sebaran normal atau mendekati normal (berbentuk setangkup, nilai yang paling banyak berada ditengah dan makin besar semakin sedikit, makin kecil makin sedikit pula, nilai-nilai ekstrim yang besar maupun yang kecil hampir tidak ada).

• Median (Nilai Tengan)

Ukuran pemusatan yang menempati posisi tengah jika data diurutkan menurut besarnya. Median adalah nilai yang berada ditengah-tengah data setelah diurutkan dari yang terkecil sampai terbesar. Median cocok digunakan bila data yang kita miliki tidak menyebar normal atau memiliki nilai yang berbeda-beda secara signifikan.

• Modus (Data Yang Sering Muncul)

Modus adalah suatu angka atau bilangan yang paling sering terjadi / muncul tetapi kalo pada data distribusi frekuensi interval modus terletak pada frekuensi yang paling besar.

• Kuartil

Kuartil adalah suatu harga yang membagi histogram frekuensi menjadi 4 bagian yang sama, sehingga disini akan terdapat 3 harga kuartil yaitu kuartil I ( K1), kuartil II (K2) dan kuartil III (K3), dimana harga kuarti II sama dengan harga median.

• Desil

Untuk kelompok data dimana n ≥ 10, dapat ditentukan 9 nilai bagian yang sama, misalnya D1, D2, … Q9, artinya setiap bagian mempunyai jumlah observasi yang sama, sedemikian rupa sehingga nilai 10% data/observasi sama atau lebih kecil dari D1, nilai 20% data/observasi sama atau lebih kecil dari D2, dan seterusnya. Nilai tersebut dinamakan desil pertama, kedua dan seterusnya sampai desil kesembilan.

• Persentil

Untuk kelompok data dimana n ≥ 100, dapat ditentukan 99 nilai, P1, P2, … P99, yang disebut persentil pertama, kedua dan ke-99, yang membagi kelompok data tersebut menjadi 100 bagian,masing-masing mempunyai bagian dengan jumlah observasi yang sama, dan sedemikian rupa sehingga 1% data/observasi sama atau lebih kecil dari P1, 2% data/observasi sama atau lebih kecil dari P2.